Discussion Topic |
|
This thread has been locked |
 Ed Hartouni
Ed Hartouni
Trad climber
Livermore, CA
|
 |
|
Jan 26, 2007 - 11:08am PT
|
one way to play this game is to take the extremes,
the stretchiest material will have a K = 0 kN,
then the impact force will be: F = 2 mg
twice the weight of the climber.
If the K -> very big,
F ~ mg*sqrt(2*f*K/(mg))
where f is the fall factor = h/L the distance of the fall h divided by the length of rope L.
Now here's a thought and a jump into complexity... you could have multiple polymer rings, each with a different K, in colors, and build a cordelette anchor attached through the rings to the anchors. For short arms you'd put a strechier ring, for long arms a stiffer ring (or no ring).
That would equalize the force...
|
|
 cintune
cintune
climber
Penn's Woods
|
 |
|
Jan 26, 2007 - 11:55am PT
|
The problem I see is that whatever stretches will bounce back, and the bigger the load, the more often, and the bigger potential variation in the angle of pull. This repeated loading and unloading of a "bungeelette" might defeat the purpose with sketchy anchors by walking them right out of their placements. Although I'm starting to sound like a broken record by now, this is the beauty of the screamer. Peak load is limited to ~2Kn, and there's no rebound to add to the uncertainty.
|
|
 Brian in SLC
Brian in SLC
Social climber
Salt Lake City, UT
|
 |
|
Jan 26, 2007 - 12:24pm PT
|
I suspect that a workable soultion is kind of polymer biner, or doughnut, that we can attatch and tie into at the power point (backed up by a sling, of course). Modern polymers are remarbably strong, and the relative stretch can be controlled in fabrication. This is a possibility worth investigating. A four inch polymer "power ring" that might stretch to, say six or eight inches under extreme loading might bear some interesting results providing it's light and sufficiently durable.
Hmmm, like a dog chew toy (or the donut ring and chew toy that some folks use to train hand strength with).
Interesting...heck, this might be KISS off the shelf easily available...
Someone oughta go to the pet or grocery store, pick one up and load test it...high loading rate, see the peak load graph type thing.
-Brian in SLC
|
|
 rgold
rgold
Trad climber
Poughkeepsie, NY
|
 |
|
Jan 26, 2007 - 12:31pm PT
|
A screamer only limits the load to 2 kN if the fall energy is completely absorbed by the time it reaches full extension. In general, I think the approximate effect of a fully extended screamer on the subsequent anchor impact is that the anchor load will be that of a five foot shorter fall.
It would follow that screamers can have a significant impact for short falls of a given fall factor, but would probably contribute little to force reduction for long falls of the same fall factor.
|
|
 Largo
Largo
Sport climber
Venice, Ca
|
 |
|
Jan 26, 2007 - 12:57pm PT
|
The "Bungeelette" has a nice ring, but I don't see it like a spring that will vault a belayer to the moon via recoil. The "dog chew" toy is closer to it but I'm just guessing.
I'm just going to have to track down something and start fiddling. The 3-point simple sling perfect equalizing plan I was so high on isn't panning out as I'd hoped. A sliding power point--in practice--works great for two points but add a third point and an change in loading invariably results in one arm going slack. This is caused by the limiter knots, without which we're looking at huge extension if one placement blows. It might be doable but after fiddling with slings for hours last night I'm starting to wonder if it isn't physically impossible to have a self-adjusting system that spans three placements. The odd number--"3"--is the bugaboo.
JL
|
|
 Ed Hartouni
Ed Hartouni
Trad climber
Livermore, CA
|
 |
|
Jan 26, 2007 - 01:27pm PT
|
ropes are designed not to bounce back...
a ring could also be... note that the ring could be a sling made of a synthetic material designed with a particular K value... doesn't have to be solid plastic...
A sceamer is an "irreversible" example of this sort of thing. I'm thinking more like a special "dog-bone"
where are the material guys?
|
|
 Ed Hartouni
Ed Hartouni
Trad climber
Livermore, CA
|
 |
|
Jan 26, 2007 - 01:37pm PT
|
here's something!
|
|
 jstan
jstan
climber
|
 |
|
Jan 26, 2007 - 01:38pm PT
|
This observation may/may not be useful. Slings and ropes are not perfectly elastic. Some energy is dissipated in the rope and leads to a rise in its temperature. Do we know how dissipative rope is? If we suppose it were perfectly dissipative the anchor question changes markedly. In that case if one anchor fails the remaining anchor(s) should only have to deal with the portion of the fall remaining. Serial failure of anchors then may be less less problematic.
We know rope is pretty dissipative. I know of no case where the falling climber rebounded to the height from which the fall originally occurred.
Edit:
Ed's graphic apparently tied the system up enough so did not see his suggestion similar to mine. What this does is change markedly the time evolution of the forces in the overall solution to the dynamical problem. It almost looks worthwhile, now, to do the dynamical problem if inelasticity can be incorporated.
You can't count on the material guys. They all just want to have fun.
|
|
 rgold
rgold
Trad climber
Poughkeepsie, NY
|
 |
|
Jan 26, 2007 - 02:24pm PT
|
Slings and ropes are not perfectly elastic. Some energy is dissipated in the rope and leads to a rise in its temperature. Do we know how dissipative rope is? If we suppose it were perfectly dissipative the anchor question changes markedly.
So would all the calculations, which so far appear to agree decently with test results. These calculations assume energy dissipated is negligible. If energy dissipation is a significant mechanism, the concept of fall factor, which is an artifact of elasticity, would probably be out the window.
In that case if one anchor fails the remaining anchor(s) should only have to deal with the portion of the fall remaining. Serial failure of anchors then may be less less problematic.
This would render moot the long-standing internet debate about whether, when a piece blows, the rope recovers significantly before it is stressed again by loading the next piece.
We know rope is pretty dissipative. I know of no case where the falling climber rebounded to the height from which the fall originally occurred.
Right, but that isn't necessarily an indication of dissipation. A more accurate mathematical model for the rope than the simple spring is probably the damped spring---critical damping would result in no recovery from maximal extension without any dissipation of energy and no beneficial effects for sequential loading. However, I have never seen an argument that, in principle, indicates why the rope should behave like a damped harmonic oscillator. Such an explanation, if there is one, might have to refer to the behavior of the polymer molecules themselves under elongation and contraction, rather than the more obvious case of internal friction, which would probably support John's idea better than the damping concept.
The Italian Alpine Club (CAI) has a sophisticated mathematical model for the entire belay chain, modeled in just this way as a system of damped harmonic oscillators.
http://www.caimateriali.org/Eventi/Torino/computermodel.html
|
|
 the Fet
the Fet
Knackered climber
A bivy sack in the secret campground
|
 |
|
Jan 26, 2007 - 04:43pm PT
|
For those of you who are interested and missed it on the rc.com slidingX thread, here is an anchor design I came up with that equalizes evenly among 3 pieces (neglecting friction, binding, etc.)(note: center piece gets the same force due to 2:1 pulley effect), limits extension, and uses just a couple extra biners.
Some problems are:
If one pieces fails then the force isn't distributed 50/50 on the remaining pieces.
Not very simple.
Biners placed in the limiter knots are untested.
Friction will limit the equalization.
But maybe this will help inspire some more ideas.
I never adopted it into my anchors beyond trying it a couple times because I think equalizing on two good pieces (with a 3rd as backup) is probably good enough, and if I did need to equalize 3 pieces I would use a slidingW and back it up with the rope or something.
|
|
 Ed Hartouni
Ed Hartouni
Trad climber
Livermore, CA
|
 |
|
Jan 26, 2007 - 05:05pm PT
|
One of the problems with the Italian Alpine Club link posted is that the physical value of the dissipation term is not given. They determined it by fitting to the accelerometer data, but didn't report the fit values.
The model is a spring and a "dash-pot," which has a term proportional to the velocity, do dissipate the energy.
I played around with this a lot to come up with the value of 600M/(m/s) for that constant, this gives a fall trajectory that seems reasonable:
x'(t) is "over" damped, x(t) is undamped
|
|
 jstan
jstan
climber
|
 |
|
Jan 26, 2007 - 05:42pm PT
|
Now why did TIG have to go and kick all this off by mentioning bounce?
When fall factor is less than 2 the biner at the top piece also provides dissipation. For a 180 degree bend at a biner I think a 30% diminution of the force is typically assumed. If you measured the temperature rise in such biner you could get an averaged caloric value for force diminution. Biners get really hot.
If ever there was a problem that cries out for use of the Method of Steepest Descent - this is it. (Just kidding.)
|
|
 WBraun
WBraun
climber
|
 |
|
Jan 26, 2007 - 05:45pm PT
|
Just see ..... the Supertopo mathematical science lab in action trying to calculated the external energy of god. At any particular time he can send the results both negative and positive outside the established rules to maintain his supremacy over all those trying to understand him without bhakti submission.
|
|
 Gene
Gene
climber
|
 |
|
Jan 26, 2007 - 05:59pm PT
|
Lots of good stuff, both theoretical and practical.
How common/how many catastrophic anchor failures occur in climbing situations? I can remember fatalities on DNB and on a desert spire over the last 5 to 10 years. Stipulated that there are many others I donít know about and one is too many, how often do anchors fail in the real world?
|
|
 healyje
healyje
Trad climber
Portland, Oregon
|
 |
|
Jan 26, 2007 - 06:06pm PT
|
ED, WTF? It's pretty and all, could you interpret for us neanderthals...?
|
|
 cintune
cintune
climber
Penn's Woods
|
 |
|
Jan 26, 2007 - 06:11pm PT
|
Werner, wouldn't prapati be more appropriate to this discussion?
|
|
 WBraun
WBraun
climber
|
 |
|
Jan 26, 2007 - 06:20pm PT
|
Gene
I would say real world anchor failures are a rarity. But when they do fail there is usually catastrophic results, duh.
Duane Raleigh as I remember had one total failure on the rappel and still lived, of course since he's still with us today. His number was not up.
Another example of the opposite. Some rescue instructor in the SF Bay Area some years ago had just finished setting up the main and belay anchors for a rescue rigging seminar. He was going to demonstrate to his class how if the main anchor system failed the belay system will back up and save the day.
He then took a knife I believe it was, and cut the main line to provide a real world, real time example in action.
Cut he did and immediately the load was transferred to the belay line in which the anchor immediately failed and he fell to his death to the witnessed shocked onlookers. Huh? His number was up.
Yes folks, strange tales from the past annals of life.
|
|
 rgold
rgold
Trad climber
Poughkeepsie, NY
|
 |
|
Jan 26, 2007 - 08:01pm PT
|
Just see ..... the Supertopo mathematical science lab in action trying to calculated the external energy of god. At any particular time he can send the results both negative and positive outside the established rules to maintain his supremacy over all those trying to understand him without bhakti submission.
God has made the desire to understand one of the central defining characteristics of the human race. Did God do this in order to have subjects for practical jokes?
|
|
 WBraun
WBraun
climber
|
 |
|
Jan 26, 2007 - 08:09pm PT
|
God has made the desire .....
No no ..... you have made the desire.
This world is created by OUR desire NOT God's desire.
|
|
 Ed Hartouni
Ed Hartouni
Trad climber
Livermore, CA
|
 |
|
Jan 26, 2007 - 08:42pm PT
|
don't know how to calculate god... leave that for Werner...
as for the plot, it has two cases, one damped, one undamped.
d2x/dt2 is the acceleration
dx/dt is the velocity
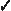 is the position. is the position.
the "primed" constant, e.g. x' is for the damped case.
In the differential equation, we have the three terms:
a*d2x/dt2 + b*dx/dt + c
which has the velocity dependent part of the model, which is the damping due to the rope.
jstan and rgold both pointed out that the rest of the anchor system has a significant effect in dissipating the energy of the fall. The analysis in my plot is for a factor 2 fall with the forces borne by the anchor, no slipping, etc.
This is not a realistic representation of a fall, but represents the extreme. It could happen if you were soloing, having tied off your anchor, and ran it out...
The point was to see what a ball park value of the "b" coefficient would be, given our fall experience is that we don't bounce on the rope. I wanted to know how much damping was required.
The constant is the "specific" constant, independent of the rope dimesions.
Maybe too much for the forum.
|
|
|
SuperTopo on the Web
|
![]() Let us know!
Let us know!